Custom infix operators are a common occurrence in Haskell. Apart from built-in operators (such as + and *), many libraries expose custom operators. For instance, Data.Monoid defines the infix operator <> as an alias for mappend.
To understand how these operators work or to create your own, you have to consider two things: Precedence and Associativity. Both of these properties are necessary for unambiguous parsing of expressions later on.
Precedence (aka Operator Binding)
Let's start with precedence because it's easier to explain. All operators in Haskell have a precedence, which is expressed with a simple integer value. 0 is the lowest possible value, whereas 9 is the highest.
Example: The expression
2 * 4 + 4 * 5 == 28isTrue, because*has a higher precedence than+(i.e.,7vs.6). Consequently, you could rewrite it as(2 * 4) + (4 * 5) == 28.
There's one crucial exception to the rule: Normal function application (i.e., space) has a precedence of 10, which is higher than the maximum definable precedence for custom infix operators.
Example: The expression
square 6 / 3 == 12isTrue, because normal function application has a higher precedence than/(i.e.,10vs.7). Consequently, you could rewrite it as(square 6) / 3 == 12.
Associativity (aka Fixity)
Associativity is less obvious, so let's first define it.
Left-Associativity: A binary operator is left-associative if and only if its applications in an expression can be grouped together from left to right without affecting the expression's meaning.
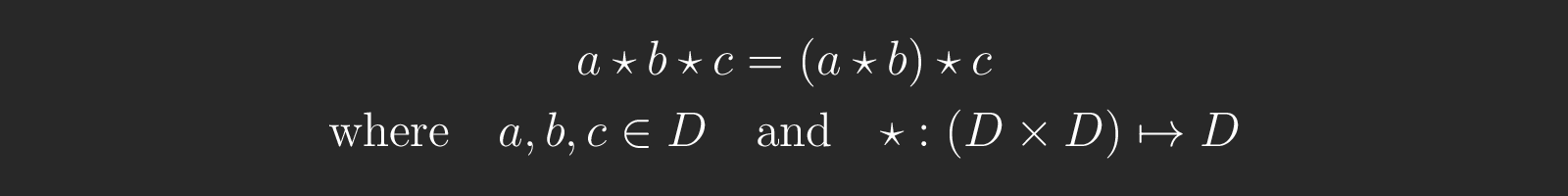
Mathematical Definition of Left-Associativity
Right-Associativity: On the other hand, if and only if the operator's applications in an expression can be grouped together from right to left, it is right-associative.
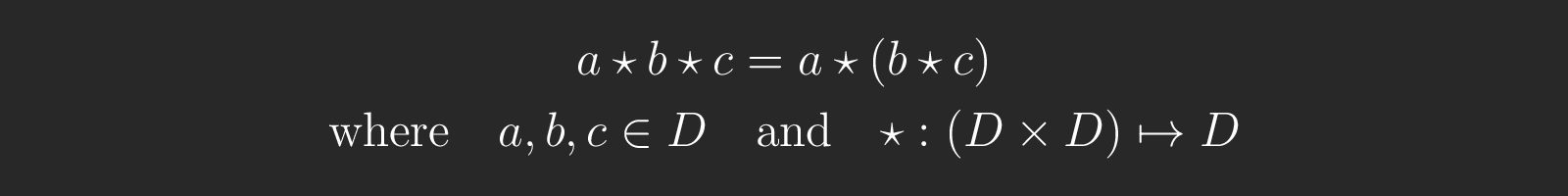
Mathematical Definition of Right-Associativity
Full-Associativity: A binary operator is fully associative if and only if it is both left- and right-associative.
In other words, the operator's applications in an expression can be arbitrarily grouped together. It doesn't matter where (or if) you place parentheses. The expression's evaluation always results in the same value.
Non-Associativity: A binary operator is non-associative if and only if it is neither left- nor right-associative.
There are three ways to define infix operators in Haskell: infixl, infixr, and infix. In the following sections, we are going to try each of these keywords by defining the operator @@ as an alias for the following function:
multiplyAndIncrement :: (Num a) => a -> a -> a
multiplyAndIncrement x y = x * y + 1
To demonstrate why precedence and associativity matter, we will evaluate the expression 2 @@ 3 @@ 3 + 1 each time (and get a different result each time).
Left-associative Operator with infixl
The following code snippet defines the left-associative operator @@ with precedence of 5:
infixl 5 @@
(@@) = multiplyAndIncrement
This scenario leads to the following evaluation of 2 @@ 3 @@ 3 + 1:
+has higher precedence than@@(i.e.,6vs.5). Therefore, the first step is to compute3 + 1, leaving us with2 @@ 3 @@ 4.@@is left-associative. Therefore, the second step is to compute2 @@ 3, leaving us with7 @@ 4.- Finally, if we apply the
@@operator again to compute7 @@ 4, we get29as our final result.
Right-associative Operator with infixr
Right-associative operator @@ with precedence of 8:
infixr 8 @@
(@@) = multiplyAndIncrement
This scenario leads to the following evaluation of 2 @@ 3 @@ 3 + 1:
@@has higher precedence than+(i.e.,8vs.5). Therefore, we have to apply@@before we apply+. Within the sub-expression2 @@ 3 @@ 3, we have to compute3 @@ 3first because of@@'s right-associativity, leaving us with2 @@ 10 + 1.- The argument from the first step still holds:
@@has higher precedence than+. So, we have to compute2 @@ 10next, leaving us with21 + 1. - Finally, if we apply the
+operator to compute21 + 1, we get22as our final result.
Non-associative Operator with infix
Non-associative operator @@ with precedence of 2:
infix 2 @@
(@@) = multiplyAndIncrement
This scenario leads to the following evaluation of 2 @@ 3 @@ 3 + 1:
+has higher precedence than@@(i.e.,6vs.2). Therefore, the first step is to compute3 + 1, leaving us with2 @@ 3 @@ 4.- Now we have a problem:
@@is non-associative, so what should our next step be?2 @@ 3or3 @@ 4?
As a matter of fact, our expression is not well defined. Unambiguous parsing is not possible. If you try to evaluate it in GHCi, it fails with an error message. Observe:
GHCi> 2 @@ 3 @@ 3 + 1
<interactive>:27:1:
Precedence parsing error
cannot mix ‘@@’ [infix 2]
and ‘@@’ [infix 2] in the
same infix expression
Conclusion
As you can see, both operator precedence and associativity may change the meaning of your program or even make it invalid.
