Generating Random Numbers for Statistics with PostgreSQL
by Christoph Schiessl on PostgreSQL
When working with statistics, generating pseudo-random samples distributed according to a given probability distribution is a frequent requirement. For me, generating these numbers directly in PostgreSQL is very convenient and improves performance in some cases. In this article, we'll look at some of the most important continuous probability distributions and implement them as SQL functions.
Uniform distribution
Uniform distributions are easy because we can use PostgreSQL's built-in RANDOM() function. RANDOM() returns uniformly distributed DOUBLE PRECISION numbers in the 0.0 <= x < 1.0 range. Adjusting that range is simply a question of adding and multiplying with appropriate values:
-- random double precision value in the range 1.0 <= x < 20.0
SELECT 1 + 19 * RANDOM();
That being said, it is easy to encapsulate that behavior in an SQL function for later reuse:
-- generates `count` uniformly distributed random numbers in the range `min <= x < max`
CREATE OR REPLACE FUNCTION random_uniform(
count INTEGER DEFAULT 1,
min DOUBLE PRECISION DEFAULT 0.0,
max DOUBLE PRECISION DEFAULT 1.0
) RETURNS SETOF DOUBLE PRECISION
RETURNS NULL ON NULL INPUT AS $$
BEGIN
RETURN QUERY SELECT min + (max - min) * RANDOM()
FROM GENERATE_SERIES(1, count);
END;
$$ LANGUAGE plpgsql;
The function's relative frequency-histogram (based on one million values):
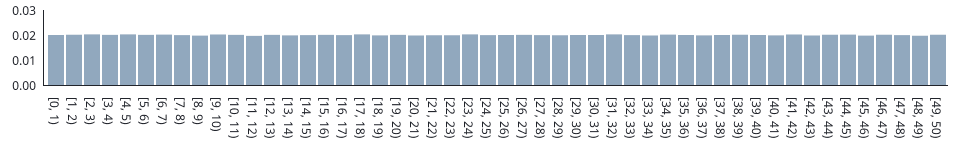
Relative frequencies have been obtained as follows: SELECT c, COUNT(r) / 1000000.0 FROM GENERATE_SERIES(0,49) AS c INNER JOIN random_uniform(1000000, 0, 50) AS r ON c = FLOOR(r) GROUP BY c ORDER BY c;
Exponential distribution
RANDOM() is the only way of generating random numbers supported by PostgreSQL. Therefore, the exponential distribution is more challenging because we must somehow derive these numbers from uniformly distributed numbers.
Since the cumulative distribution function of the exponential distribution is invertible, we can use a technique known as inverse transform sampling. All of this boils down to a simple mathematical expression that we can encapsulate in another SQL function:
-- generates `count` exponentially distributed random numbers with a given expected value
CREATE OR REPLACE FUNCTION random_exp(
count INTEGER DEFAULT 1,
mean DOUBLE PRECISION DEFAULT 1.0
) RETURNS SETOF DOUBLE PRECISION
RETURNS NULL ON NULL INPUT AS $$
DECLARE
u DOUBLE PRECISION;
BEGIN
WHILE count > 0 LOOP
u = RANDOM(); -- range: 0.0 <= u < 1.0
IF u != 0.0 THEN
RETURN NEXT -LN(u) * mean;
count = count - 1;
END IF;
END LOOP;
END;
$$ LANGUAGE plpgsql;
The function's relative frequency-histogram (based on one million values):
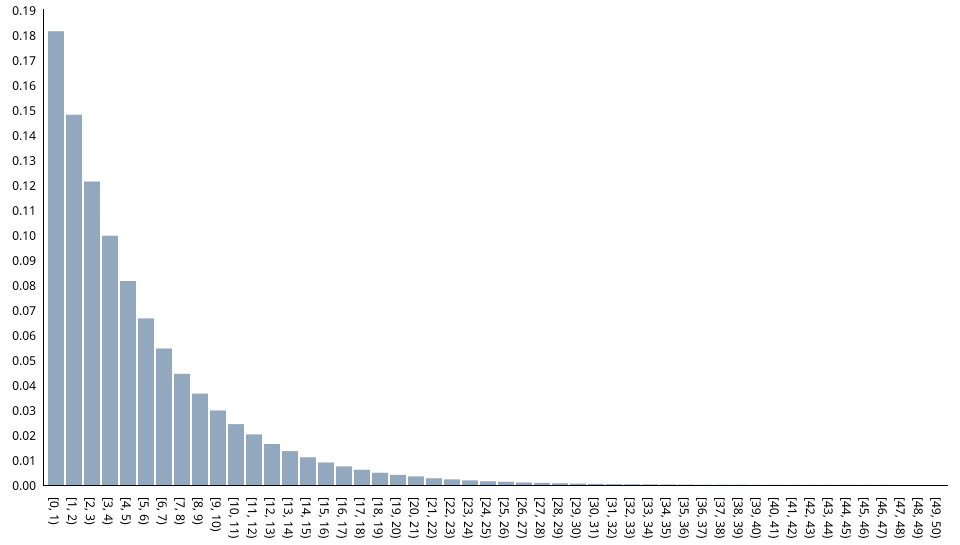
Relative frequencies have been obtained as follows: SELECT c, COUNT(r) / 1000000.0 FROM GENERATE_SERIES(0,49) AS c INNER JOIN random_exp(1000000, 5) AS r ON c = FLOOR(r) GROUP BY c ORDER BY c;
Normal distribution
The normal distribution is probably the most important of all continuous distributions.
We must again derive them from uniformly distributed numbers to generate normally distributed numbers. Fortunately, mathematicians have discovered many ways of doing exactly that: Central limit theorem, Box-Muller transform, Marsaglia polar method, ...
For now, I've decided to implement the Marsaglia polar method because it's reasonably simple to implement in SQL:
-- generates `count` normally distributed random numbers with a given mean and standard deviation
CREATE OR REPLACE FUNCTION random_normal(
count INTEGER DEFAULT 1,
mean DOUBLE PRECISION DEFAULT 0.0,
stddev DOUBLE PRECISION DEFAULT 1.0
) RETURNS SETOF DOUBLE PRECISION
RETURNS NULL ON NULL INPUT AS $$
DECLARE
u DOUBLE PRECISION;
v DOUBLE PRECISION;
s DOUBLE PRECISION;
BEGIN
WHILE count > 0 LOOP
u = RANDOM() * 2 - 1; -- range: -1.0 <= u < 1.0
v = RANDOM() * 2 - 1; -- range: -1.0 <= v < 1.0
s = u^2 + v^2;
IF s != 0.0 AND s < 1.0 THEN
s = SQRT(-2 * LN(s) / s);
RETURN NEXT mean + stddev * s * u;
count = count - 1;
IF count > 0 THEN
RETURN NEXT mean + stddev * s * v;
count = count - 1;
END IF;
END IF;
END LOOP;
END;
$$ LANGUAGE plpgsql;
The function's relative frequency-histogram (based on one million values) clearly shows that the generated numbers are indeed normally distributed (with an expected value of 25 and a standard deviation of 7):
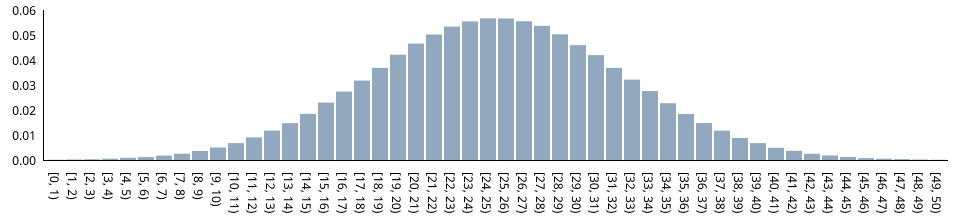
Relative frequencies have been obtained as follows: SELECT c, COUNT(r) / 1000000.0 FROM GENERATE_SERIES(0,49) AS c INNER JOIN random_normal(1000000, 25, 7) AS r ON c = FLOOR(r) GROUP BY c ORDER BY c;
That's it for today! Thank you for reading, and see you soon!

